1) Hemos comprado 3 kg de manzanas y nos han cobrado 3,45 €. ¿Cuánto nos
cobrarían por 1, 2, 5 y 10 kg?
2) Marta ha cobrado por repartir propaganda durante cinco días 126 €. ¿Cuántos días
deberá trabajar para cobrar 340,2 €?
3) En un plano de una ciudad, una calle de 350 metros de longitud mide 2,8 cm.
¿Cuánto medirá sobre ese mismo plano otra calle de 200 metros?
4) En una panadería, con 80 kilos de harina hacen 120 kilos de pan. ¿Cuántos kilos de
harina serían necesarios para hacer 99 kilos de pan?
5) Ana medía 1,42 m a principios de año. Pasados tres meses, medía 1,45 y a finales de
año, 1,51. ¿Cuándo creció más rápido, en los primeros tres meses o en el resto del
año?
6) En el equipo de fútbol del barrio han jugado como porteros Ángel y Diego. A Ángel
le han marcado 13 goles en 10 partidos jugados. Diego jugó 15 partidos y le
marcaron 18 goles. ¿Cuál de los dos ha tenido mejores actuaciones?
7) Una piscina portátil ha tardado en llenarse seis horas utilizando cuatro grifos
iguales. ¿Cuántos grifos, iguales a los anteriores, serían necesarios para llenarla en 3
horas?
8) Para construir una casa en ocho meses han sido necesarios seis albañiles. ¿Cuántos
habrían sido necesarios para construir la casa en tan sólo tres meses?
9) En una fábrica automovilística, una máquina pone, en total, 15.000 tornillos en las 8
horas de jornada laboral, funcionando de forma ininterrumpida. ¿Cuántos tornillos
pondrá en 3 horas?
10) Después de una fuerte tormenta, dos autobombas han tardado 6 horas en desaguar
un garaje que se había anegado. ¿Cuántas horas se hubiera tardado utilizando sólo 3
autobombas?
11) Un coche ha tardado 42 minutos en recorrer 70 km. Suponiendo que va a la misma
velocidad, contesta a las siguientes cuestiones:
a) ¿Cuánto tardará en recorrer 150 km?
b) ¿Cuántos kilómetros recorrerá en dos horas y tres minutos?
12) Un automóvil ha tardado en hacer el recorrido Madrid-Zaragoza tres horas y cuarto
a una media de 100 km/h. ¿Cuánto tardará un autobús a una media de 90 km/h?
1) 1,15 €; 2,30 €; 5,75 € y 11,5 € respectivamente. 2) 13,5 días 3) 1,6 cm
4) 66 kg de harina. 5) En los primeros 3 meses (1 cm/mes) 6) Diego:1,2 goles por partido
7) 8 grifos 8) 16 albañiles 9) 5.625 tornillos. 10) 4 horas
11) a) 90 minutos b) 205 km 12) 175,5 minutos = 2 h 55 min 30 seg
martes, 8 de marzo de 2016
1) Hemos comprado 3 kg de manzanas y nos han cobrado 3,45 €. ¿Cuánto nos
cobrarían por 1, 2, 5 y 10 kg?
2) Marta ha cobrado por repartir propaganda durante cinco días 126 €. ¿Cuántos días deberá trabajar para cobrar 340,2 €?
3) En un plano de una ciudad, una calle de 350 metros de longitud mide 2,8 cm. ¿Cuánto medirá sobre ese mismo plano otra calle de 200 metros?
4) En una panadería, con 80 kilos de harina hacen 120 kilos de pan. ¿Cuántos kilos de harina serían necesarios para hacer 99 kilos de pan?
5) Ana medía 1,42 m a principios de año. Pasados tres meses, medía 1,45 y a finales de año, 1,51. ¿Cuándo creció más rápido, en los primeros tres meses o en el resto del año?
6) En el equipo de fútbol del barrio han jugado como porteros Ángel y Diego. A Ángel le han marcado 13 goles en 10 partidos jugados. Diego jugó 15 partidos y le marcaron 18 goles. ¿Cuál de los dos ha tenido mejores actuaciones?
7) Una piscina portátil ha tardado en llenarse seis horas utilizando cuatro grifos iguales. ¿Cuántos grifos, iguales a los anteriores, serían necesarios para llenarla en 3 horas?
8) Para construir una casa en ocho meses han sido necesarios seis albañiles. ¿Cuántos habrían sido necesarios para construir la casa en tan sólo tres meses?
9) En una fábrica automovilística, una máquina pone, en total, 15.000 tornillos en las 8 horas de jornada laboral, funcionando de forma ininterrumpida. ¿Cuántos tornillos pondrá en 3 horas?
10) Después de una fuerte tormenta, dos autobombas han tardado 6 horas en desaguar un garaje que se había anegado. ¿Cuántas horas se hubiera tardado utilizando sólo 3 autobombas?
11) Un coche ha tardado 42 minutos en recorrer 70 km. Suponiendo que va a la misma velocidad, contesta a las siguientes cuestiones: a) ¿Cuánto tardará en recorrer 150 km? b) ¿Cuántos kilómetros recorrerá en dos horas y tres minutos?
12) Un automóvil ha tardado en hacer el recorrido Madrid-Zaragoza tres horas y cuarto a una media de 100 km/h. ¿Cuánto tardará un autobús a una media de 90 km/h?
SOLUCIONES:
1) 1,15 €; 2,30 €; 5,75 € y 11,5 € respectivamente.
2) 13,5 días
3) 1,6 cm
4) 66 kg de harina.
5) En los primeros 3 meses (1 cm/mes)
6) Diego:1,2 goles por partido
7) 8 grifos
8) 16 albañiles
9) 5.625 tornillos.
10) 4 horas
11) a) 90 minutos b) 205 km
12) 175,5 minutos = 2 h 55 min 30 seg
2) Marta ha cobrado por repartir propaganda durante cinco días 126 €. ¿Cuántos días deberá trabajar para cobrar 340,2 €?
3) En un plano de una ciudad, una calle de 350 metros de longitud mide 2,8 cm. ¿Cuánto medirá sobre ese mismo plano otra calle de 200 metros?
4) En una panadería, con 80 kilos de harina hacen 120 kilos de pan. ¿Cuántos kilos de harina serían necesarios para hacer 99 kilos de pan?
5) Ana medía 1,42 m a principios de año. Pasados tres meses, medía 1,45 y a finales de año, 1,51. ¿Cuándo creció más rápido, en los primeros tres meses o en el resto del año?
6) En el equipo de fútbol del barrio han jugado como porteros Ángel y Diego. A Ángel le han marcado 13 goles en 10 partidos jugados. Diego jugó 15 partidos y le marcaron 18 goles. ¿Cuál de los dos ha tenido mejores actuaciones?
7) Una piscina portátil ha tardado en llenarse seis horas utilizando cuatro grifos iguales. ¿Cuántos grifos, iguales a los anteriores, serían necesarios para llenarla en 3 horas?
8) Para construir una casa en ocho meses han sido necesarios seis albañiles. ¿Cuántos habrían sido necesarios para construir la casa en tan sólo tres meses?
9) En una fábrica automovilística, una máquina pone, en total, 15.000 tornillos en las 8 horas de jornada laboral, funcionando de forma ininterrumpida. ¿Cuántos tornillos pondrá en 3 horas?
10) Después de una fuerte tormenta, dos autobombas han tardado 6 horas en desaguar un garaje que se había anegado. ¿Cuántas horas se hubiera tardado utilizando sólo 3 autobombas?
11) Un coche ha tardado 42 minutos en recorrer 70 km. Suponiendo que va a la misma velocidad, contesta a las siguientes cuestiones: a) ¿Cuánto tardará en recorrer 150 km? b) ¿Cuántos kilómetros recorrerá en dos horas y tres minutos?
12) Un automóvil ha tardado en hacer el recorrido Madrid-Zaragoza tres horas y cuarto a una media de 100 km/h. ¿Cuánto tardará un autobús a una media de 90 km/h?
SOLUCIONES:
1) 1,15 €; 2,30 €; 5,75 € y 11,5 € respectivamente.
2) 13,5 días
3) 1,6 cm
4) 66 kg de harina.
5) En los primeros 3 meses (1 cm/mes)
6) Diego:1,2 goles por partido
7) 8 grifos
8) 16 albañiles
9) 5.625 tornillos.
10) 4 horas
11) a) 90 minutos b) 205 km
12) 175,5 minutos = 2 h 55 min 30 seg
Qué es la proporcionalidad directa e inversa?
Existen 3 tipos de proporcionalidad:
A) Proporción Directa
Dos cantidades a y b son directamente proporcionales si al aumentar o disminuir una de ellas, la otra aumenta o disminuye el mismo número de veces.
Se le simboliza como a=kb ( k =cte. de proporcionalidad)
Los cocientes que forman una proporción directa tienen siempre un valor constante.
Su gráfica es una línea recta que pasa por el origen.
B) Proporción Inversa
Dos cantidades, a y b, son Inversamente Proporcionales cuando haciéndose mayor o menor la primera cantidad, la segunda se hace menor o mayor el mismo número de veces.
Se le simboliza como a=k(1/b) (k = cte.de proporcionalidad)
El producto de dos cantidades inversamente proporcionales es siempre constante.
Su gráfica es asintótica al eje x.
C) Proporción Compuesta
Se presenta como una combinación de Proporciones Directas e Inversas.
Diremos que un problema es de proporcinalidad compuesta si intervienen tres o más magnitudes. Al intervener más de dos magnitudes las relaciones proporcinales dos a dos de las magnitudes pueden ser distintas, es decir, si tenemos las magnitudes A, B y C, la relación proporcinal entre A y B puede ser directa o inversa y entre B y C puede ocurrir lo mismo
A) Proporción Directa
Dos cantidades a y b son directamente proporcionales si al aumentar o disminuir una de ellas, la otra aumenta o disminuye el mismo número de veces.
Se le simboliza como a=kb ( k =cte. de proporcionalidad)
Los cocientes que forman una proporción directa tienen siempre un valor constante.
Su gráfica es una línea recta que pasa por el origen.
B) Proporción Inversa
Dos cantidades, a y b, son Inversamente Proporcionales cuando haciéndose mayor o menor la primera cantidad, la segunda se hace menor o mayor el mismo número de veces.
Se le simboliza como a=k(1/b) (k = cte.de proporcionalidad)
El producto de dos cantidades inversamente proporcionales es siempre constante.
Su gráfica es asintótica al eje x.
C) Proporción Compuesta
Se presenta como una combinación de Proporciones Directas e Inversas.
Diremos que un problema es de proporcinalidad compuesta si intervienen tres o más magnitudes. Al intervener más de dos magnitudes las relaciones proporcinales dos a dos de las magnitudes pueden ser distintas, es decir, si tenemos las magnitudes A, B y C, la relación proporcinal entre A y B puede ser directa o inversa y entre B y C puede ocurrir lo mismo
viernes, 4 de marzo de 2016
MULTIPLICAR NUMEROS FRACCIONADOS
Hay 3 simples pasos para multiplicar fracciones
1. Multiplica los números de arriba (los numeradores).
2. Multiplica los números de abajo (los denominadores).
3. Simplifica la fracción. |
Ejemplo 1
| 1 | × | 2 |
| 2 | 5 |
| 1 | × | 2 | = | 1 × 2 | = | 2 |
| 2 | 5 |
Paso 2. Multiplica los números de abajo:
| 1 | × | 2 | = | 1 × 2 | = | 2 |
| 2 | 5 | 2 × 5 | 10 |
Paso 3. Simplifica la fracción:
| 2 | = | 1 |
| 10 | 5 |
Ejemplo 2
| 1 | × | 9 |
| 3 | 16 |
| 1 | × | 9 | = | 1 × 9 | = | 9 |
| 3 | 16 |
Paso 2. Multiplica los números de abajo:
| 1 | × | 9 | = | 1 × 9 | = | 9 |
| 3 | 16 | 3 × 16 | 48 |
Paso 3. Simplifica la fracción:
| 9 | = | 3 |
| 48 | 16 |
EJERCICIOS DE SUMA Y RESTAS DE FRACCIONES
| 1 | 2 | + | 1 | = | |
| 5 | 5 | 5 |
| 2 | 6 | − | 4 | = | |
| 7 | 7 | 7 |
| 3 | 1 | + | 2 | = | |
| 5 | 3 | 15 |
mcm (3,5) = 5 · 3 = 15
| 4 | 5 | + | 3 | = | |
| 6 | 20 | 60 |
mcm(6,20) = 22 · 3 · 5 = 60
| 5 | 7 | + | 3 | = | |
| 10 | 4 |
mcm(10,4) = 22 · 5 = 20
| 6 | 7 | − | 5 | = | |
| 8 | 12 |
mcm(8,12) = 23 · 3 = 24
FRACCIONES EQUIVALENTES
Fracciones equivalentes
Las fracciones equivalentes son aquellas fracciones que representan una misma cantidad. Por ejemplo, ¿cuál de las siguientes fracciones crees que será mayor?

¿Lo has averiguado? Vamos a verlo con un ejemplo, partiendo esta pizza en tantos trozos como indique la fracción.
Para representar 1/2, partiremos la pizza en 2 trozos y nos quedaremos con 1 trozo:

Para representar 3/6, partiremos la pizza en 6 trozos y nos quedaremos con 3 trozos:
Para representar 4/8, partiremos la pizza en 8 trozos y nos quedaremos con 4 trozos:
¿Hay algún trozo de pizza que sea más grande? ¡No! Fíjate, las tres fracciones representan la misma cantidad de pizza, justo la mitad, por eso son fracciones equivalentes:
¿Cómo sabemos si dos fracciones son equivalentes? Dos fracciones son equivalentes si representan el mismo número decimal.
Por ejemplo, las tres fracciones anteriores representan el mismo número decimal: 0,5.
1/2 es 1 entre 2, que es 0,5.

3/6 es 3 entre 6, que es 0,5.
4/8 es 4 entre 8, que es 0,5.
¿Cómo podemos hallar una fracción que sea equivalente a otra?
Si queremos hallar una fracción equivalente a otra, podemos:
– Multiplicar denominador y numerador por el mismo número. Hallamos una fracción equivalente con números más grandes. Por eso este proceso se llama amplificación.
– Dividir denominador y numerador por el mismo número (ambos deben ser divisibles por este número). Así, estamos hallando una fracción equivalente con números más pequeños. Por eso, este proceso se llama simplificación.

¿Estás listo para practicar algunos ejercicios de fracciones equivalentes? Pues pincha en los siguientes enlaces:
Practica ejercicios de fracciones equivalentes
Practica ejercicios de fracciones equivalentes más difíciles
martes, 1 de marzo de 2016
PROPORCIONES PARA BIZCOCHO PROTEICO

Ingredientes:
- Avena o Weetabix.
- Claras de Huevo.
- Queso Fresco Batido 0%.
- Whey de sabor a gusto del consumidor.
- Canela (Opcional).
- Frutos secos (Opcional).
- Frutas Deshidratadas como pasas, orejones, higos, dátiles,… (Opcional).
Nota: Las cantidades varían según los requerimientos de cada persona, pero dejando como muestra, en las siguientes capturas, los ingredientes utilizados fueron:
- 80gr avena o 4 unidades de Weetabix.
- 250ml de claras.
- 250gr de Queso Fresco Batido 0%.
- 1 scoop de Whey.
- 30-40gr de frutos secos (nueces, almendras, avellanas).
- 1 cuchara de canela en polvo.
Preparación:
En un vaso de batidora añadimos las claras de huevo, la avena o weetabix, y la proteína whey.
Batimos hasta que todo quede bien molido y mezclado. Añadimos la canela y frutos secos una vez batido y removemos con una cuchara
Vertemos todo la mezcla en un bol apto para microondas. Calentaremos la preparación durante 5-8 minutos a máxima potencia. Aquí puede variar según el microondas, la recomendación es que se establezca el mínimo tiempo (5 minutos), se introduzca un cuchillo en el bizcocho para observar si está bien hecho. En el caso que no lo esté seguir calentando durante períodos de 2 minutos e ir observando.
Una vez listo, bien se puede comer en caliente bien puede ser enfriado para tomar más tarde. En el caso del ejemplo, lo que suelo hacer es dividir el bizcocho en dos mitades, comiendo una en el desayuno y la otra en la merienda.
Para los más “golosos”, se puede cubrir con un poco de miel, perfectamente factible para un post entreno que haya sido demandante. Queso para untar es muy buena opción.
Observar las formas curiosas que adopta cada bizcocho según el molde usado. En el foro en el que me muevo (www.musclecoop.com) se les denomina “Bollo-Truño”, término inventado por el forero “Supevic”. Ya podéis intuir el por qué del nombre, :P.
MINIMO COMUN
Precisiones[editar]
Si a y b son números enteros distintos de cero y si el número c es de modo que c|a y a su vez c|b, a este número c se denomina divisor común de los números a y b.1 Obsérvese que dos números enteros cualesquiera tienen divisores comunes. Cuando existen, únicamente, como divisores comunes 1 y -1 de los números a y b, estos se llaman primos entre sí.
Un número entero d se llama máximo común divisor (MCD) de los números a y b cuando:
- d es divisor común de los números a y b y
- d es divisible por cualquier otro divisor común de los números a y b.
Ejemplo:
- 12 es el mcd de 36 y 60. Pues 12|36 y 12|60; a su vez 12 es divisible por 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 12 y -12 que son divisores comunes de 36 y 60.2
Cálculo del MCD[editar]
Los tres métodos más utilizados para el cálculo del máximo común divisor de dos números son:
Por descomposición en factores primos[editar]
Artículo principal: Factorización de enteros
El máximo común divisor de dos números puede calcularse determinando la descomposición en factores primos de los dos números y tomando los factores comunes elevados a la menor potencia, el producto de los cuales será el MCD.
Ejemplo: para calcular el máximo común divisor de 48 y de 60 se obtiene de su factorización en factores primos.
|
|
|
El MCD son los factores comunes con su menor exponente, esto es:
En la práctica, este método solo es operativo para números pequeños tomando en general demasiado tiempo calcular la descomposición en factores primos de dos números cualquiera.
Usando el algoritmo de Euclides[editar]
Artículo principal: Algoritmo de Euclides
Un método más eficiente es el algoritmo de Euclides, que utiliza el algoritmo de la división junto al hecho que el MCD de dos números también divide al resto obtenido de dividir el mayor entre el más pequeño.
Ejemplo 1:
Si se divide 60 entre 48 dando un cociente de 1 y un resto de 12, el MCD será por tanto divisor de 12. Después se divide 48 entre 12 dando un resto de 0, lo que significa que 12 es el MCD. Formalmente puede describirse como:
Ejemplo 2:
El MCD de 42 y 56 es 14. En efecto:
operando:
Usando el mínimo común múltiplo[editar]
El máximo común divisor también puede ser calculado usando el mínimo común múltiplo. Si a y b son distintos de cero, entonces el máximo común divisor de a y b se obtiene mediante la siguiente fórmula, que involucra el mínimo común múltiplo de a y b:
MCD de tres o más números[editar]
Propiedades[editar]
1. Si  entonces
entonces 
 entonces
entonces 
2. Si  es un entero,
es un entero, 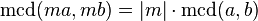
 es un entero,
es un entero, 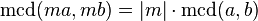
3. Si  es un número primo, entonces
es un número primo, entonces  o bien
o bien 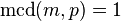
 es un número primo, entonces
es un número primo, entonces  o bien
o bien 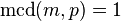
4. Si 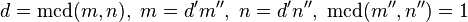 , entonces
, entonces 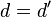
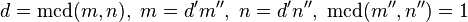 , entonces
, entonces 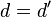
5. Si  es un divisor común de
es un divisor común de  y
y  , entonces
, entonces 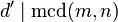
 es un divisor común de
es un divisor común de  y
y  , entonces
, entonces 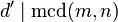
6. Si  , entonces
, entonces 
 , entonces
, entonces 
7. Si 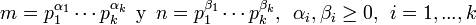 , entonces:
, entonces:
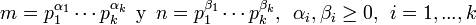 , entonces:
, entonces:
La última propiedad indica que el máximo común divisor de dos números resulta ser el producto de sus factores primos comunes elevados al menor exponente.
Geométricamente, el máximo común divisor de a y b es el número de puntos de coordenadas enteras que hay en el segmento que une los puntos (0,0) y (a,b), excluyendo el (0,0).
Proposiciones[editar]
- Para cualquier par de números enteros a≠0, b≠0, existe un único mcd d ≥ 1.5
- El m.c.d. de los números a y b puede ser representado en forma de combinación lineal de estos números. Esto es (a, b) = ax + by
- Si dos números enteros son primos entre sí, i.e. su mcd = 1 o en otra notación (a,b) = 1, entonces cabe la representación ma + nb = 1 donde m y n son números enteros (Identidad de Bézout).
- si a|bc y (a,b) = 1, será a|c. En otras palabras, si un número a divide un producto de otros dos números y es coprimo con uno de ellos, entonces divide necesariamente el otro número o factor.6
- Cuando un número a es coprimo con los números m y n, también lo es con el producto mn.7
- (a,b) es divisor de (a, bc)8
- t(a,b) = (ta, tb) para todo t entero9
- Si (m, b)= 1 entonces (am, b)= (a, b)10
- Si (m,b)= 1, (am, n) = 1 entones (am, bn) = (a, b)
- Para todo x, (a, b)= (b, a) = (a, -b) = (a, b + ax)11
- " Por definición, (0, 0) = 0 ".12 De tal modo el mcd se definiría en todo ℤxℤ.
- (a, b) = b si sólo si b | a, ( O sea si a es múltiplo de b).
- si (a,b)= D, entonces (an, bn) = Dn13
- mZ + nZ = (m,n)Z. Si sumamos sendos múltiplos de dos enteros es lo mismo que considerar los múltiplos de su máximo común divisor.14
 15
15
MCD como operación interna[editar]
- EL Mcd se puede estructurar como una operación en ℤ, de este modo a cualquier par de enteros, o sea a un elemento de ℤxℤ le asigna un único elemento de ℤ.
- Para cualquier par de enteros (a,b) existe un entero no negativo d que es su máximo común divisor. Esto es a*b = (a,b) = d
- El MCD goza de la propiedad asociativa, como de la propiedad conmutativa.
- El mcd posee un elemento identidad, el cero, de modo tal que (a, 0)= (0,a)= a16
- El mcd tiene un comportamiento dual que el mínimo común múltiplo y a los enteros no negativos a y b los liga la ecuación ab = (a,b)[a,b]17
- Propiedad de 1: (a,1) = 1 para cualquier entero a18
REGLA DE TRES INVERSA
Consiste en que dadas dos cantidades correspondientes a magnitudes inversamente proporcionales, calcular la cantidad de una de estas magnitudes correspondiente a una cantidad dada de la otra magnitud.
La regla de tres inversa la aplicaremos cuando entre las magnitudes se establecen las relaciones:
A más  menos.
menos.
A menos  más.
más.
Ejemplos:


Un grifo que mana 18 l de agua por minuto tarda 14 horas en llenar un depósito. ¿Cuánto tardaría si su caudal fuera de 7 l por minuto?
Son magnitudes inversamente proporcionales, ya que a menos litros por minuto tardarámás en llenar el depósito.
18 l/min  14 h
14 h
7 l/min  x h
x h
3 obreros construyen un muro en 12 horas, ¿cuánto tardarán en construirlo 6 obreros?
Son magnitudes inversamente proporcionales, ya que a más obreros tardarán menoshoras.
3 obreros  12 h
12 h
6 obreros  x h
x h
Suscribirse a:
Comentarios (Atom)



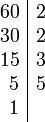
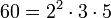

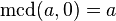

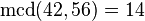


 .
.